▶ 구 외부에서의 전기장 값
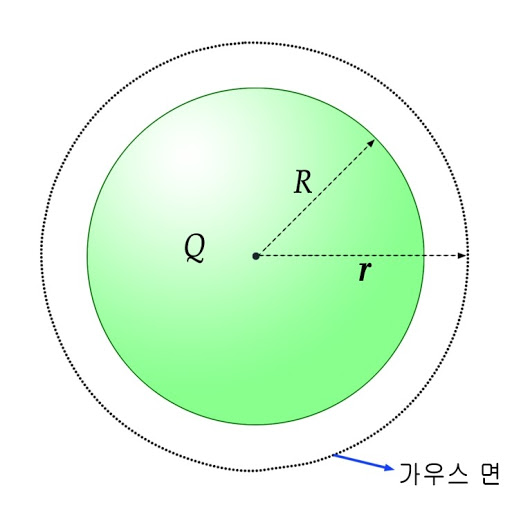
보시면 Q는 균일하게 꽉 찬 구에서의 전체 전하량입니다. R은 전하의 반지름이고 r은 구로부터 떨어진 거리를 의미합니다. 우리는 r만큼 떨어진 어느 지점을 P라고 하겠습니다. P점에서의 전기장을 구하면 되는 것입니다.
구 외부에서의 전기장 값을 구하는 법은 쉽습니다. 그냥 구를 하나의 '점전하'로 인식하면 되거든요. 위 그림에서는 r의 크기가 R과 차이가 안나보이지만요 ㅎㅎ 어쨌든, 먼저 적분꼴 가우스 법칙을 가져와서 생각해보도록 합시다.

자, 이 상태에서 dA는 뭐죠? 구의 미소면적이죠? 근데 이 미소면적에 적분을 붙여주면 결국 구의 표면적을 의미합니다.
근데 우리가 이전 포스팅에서 공부했듯이, Flux의 총량은 구의 표면에서의 적분값과 같다고 했습니다. 따라서, 지금 우리는 r만큼 떨어진 거리에서 '임의의 가우스 폐곡면'을 그려주었으니, 반지름이 r인 구의 표면적을 구하면 되는 것입니다.
이걸 '구각 정리 (구껍질 정리)' 라고 부릅니다.
그러면 dA를 적분한 값은 4πr^2이 되겠습니다. 따라서, 구 외부에서의 전기장은 다음 값을 가지게 됩니다.
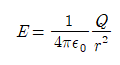
▶ 구 내부에서의 전기장 값
- 자, 이번에는 구 내부에서의 전기장 값입니다.
얘는 좀 어렵습니다.
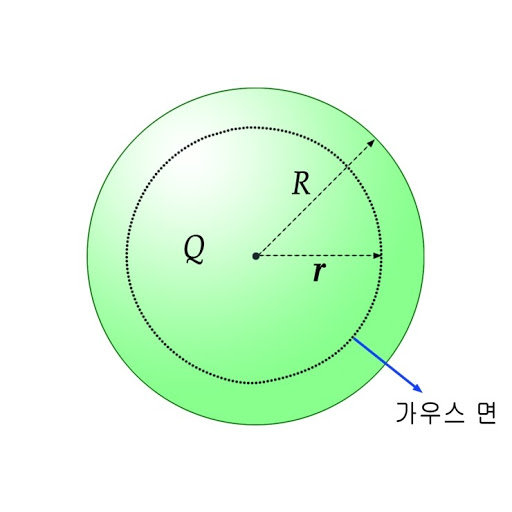
이러한 모습이죠? 얘는 부피 전하 밀도를 사용할것입니다. 여기서도 구껍질 정리를 적용할 수 있습니다. 이번에는 구의 껍질이 반지름이 R인 구가 되겠습니다.

여러분들이 이미 알고 계시겠지만 내부가 균일하게 꽉 찬 구라는 것은 '부도체' 구임을 의미합니다. 만약 도체 구라면 구 내부의 전기장 값은 0입니다. 대전된 상태의 구는 전하들이 구의 표면으로 전부 이동하기 때문이지요.
아무튼 이쪽 파트는 일반물리2에서도 배우셨겠지만 전자기학에서도 그대로 재탕할만큼 매우 중요한 파트이므로, 열심히 공부하시길 바랍니다.
+ 추가로 설명드릴게 하나 있어서 이어 적습니다. 바로 부도체 구에서의 내부와 표면, 외부에 따른 전기장값의 그래프인데요.
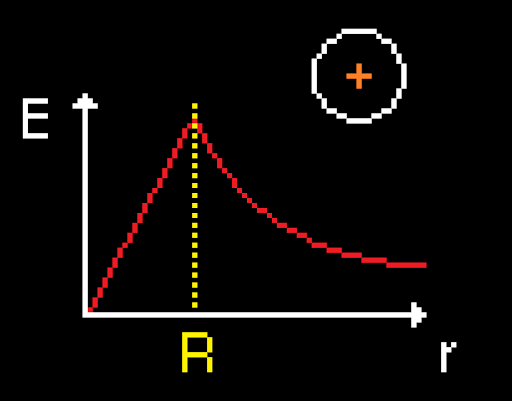
이런 꼴의 그래프를 보이게 됩니다. 보시면 구 내부에서는 거리에 따라 직선형태로 전기장이 증가하다가 '표면'에서 최고점을 찍고 외부로 나가게 되는 순간부터는 거리와 전기장의 크기가 서로 반비례하는 모습을 보이고 있습니다. 이는 나중에 전위를 공부할 때 전위그래프와 함께 비교하며 다시 나오게될 것입니다.
'대학물리 > 일반물리 - [전자기학]' 카테고리의 다른 글
| [전자기학] 전기 퍼텐셜 에너지 & 전기 퍼텐셜(전위) / 길이가 무한한 도선에서의 전위 값 구하기 (0) | 2020.04.04 |
|---|---|
| [전자기학] 무한 막대 전하(원통형 도선)와 무한한 평면판에서의 전기장 값 구하기 (0) | 2020.04.03 |
| [전자기학] 적분형 가우스 법칙표현 & 미분형 가우스 법칙표현 / 발산정리(Divergence Theorem)에 대하여 (0) | 2020.04.02 |
| [전자기학] 고리 전하에서의 전기장 값 구하기 (0) | 2020.04.02 |
| [전자기학] 쿨롱의 법칙(Coulomb's law) 과 중첩의 원리 & 연속적인 전하분포에서의 전기장 값 구하기 (길이 전하) (2) | 2020.04.02 |



