▶ 크로네커 델타 (Cronecker Delta)
크로네커 델타는 다음의 정의를 가집니다.

i성분과 j성분이 같으면 1, 아니면 0으로 이를 33행렬식으로 표현했을 때, 위와 같이 단위행렬의 모습을 띠고 있음을 보여줍니다. 크로네커 델타에 대한 또 다른 성질로는 두 성분의 위치가 바껴도 같은 값을 가진다는 것입니다.
예를 들면 δ_ij에서 행렬의 위치를 (1,1) (1,2) (1,3) (2,1) (2,2) (2,3) (3,1) (3,2) (3,3)로 나타내었을 때, (1,2)=(2,1)라는 예시와 같이 같은 값을 가짐을 알 수 있습니다. 즉, 전치행렬과 기존의 행렬이 같다는 것을 의미합니다.
한가지 더 특징이 있습니다. 이 크로네커델타에다가 벡터성분을 곱해주면 다음과 같은 성질을 가집니다.

이러한 값을 가지는데요. 첫번째 예시를 보면 델타j와 벡터j는 Dummy Index이기 때문에 사라지고 v_i만 남게 됩니다.
이는 벡터뿐만 아니라 또 다른 크로네커 델타를 곱해줘도 같은 방법으로 적용됩니다.
그러면 크로네커델타와 벡터의 곱을 통해 단위 행렬을 표현해보도록 하겠습니다.
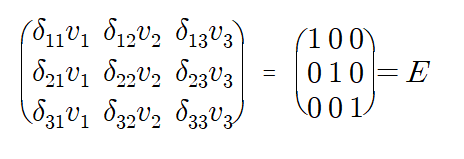
이렇게 나옵니다. 지금 첫번째 성질의 예시를 든 것입니다. 위에서 말했듯이 크로네커델타는 각 성분이 같으면 1 아니면 0이기 때문에 저러한 값이 나오구요. j와j성분은 같으므로 더미인덱스라서 v_i 형태로 도출되어 위처럼 단위행렬이 나오게 되었습니다.
▶ 레비치비타 텐서 (Levi-Civita Tensor)
레비치비타 텐서는 입실론으로 표현합니다. 아래와 같은 형태를 띱니다.

레비치비타 텐서가 1을 가질 경우에는 i,j,k의 배열이 저런식이면 됩니다. 규칙이 보이시나요? 123에서 1을 맨 뒤로 옮기면 231이고 여기서 다시 한번 2를 맨 뒤로 옮기면 312입니다. 이걸 다시 3을 맨 뒤로 옮기면 처음의 123으로 돌아오게 됩니다. 정삼각형이 있고 위쪽 꼭짓점을 i , 오른쪽 꼭짓점을 j , 왼쪽 꼭짓점을 k라고 둘 경우 시계방향으로 회전하는 배열은 레비치비타 텐서가 1값을 가진다는 것을 알 수 있겠습니다.
그러면 -1인 경우도 여러분들이 적용할 수 있을 것입니다.

그러면 만약 ε의 배열이 123인 상태에서 12를 서로 바꿔줘 봅시다. 그러면 213이죠? 이렇게 한 번 자리를 바꿀때마다 부호가 바뀌게 되는 것도 알아두시면 좋습니다.
그러면 우리는 대체 왜 이걸 배워야하느냐? 이게 바로 벡터 외적과 내적의 시초이기 때문입니다.
레비치비타 텐서를 통해서 벡터외적을 표현할 수가 있는데요.

대충 이러한 모습입니다. 그러면 이걸 가지고 몇가지 예제를 증명해보고자 합니다.

https://blog.naver.com/twonkang00/221973217939
수정 2020_05_21 2번에 대한 증명은 사실 증명이라기보다는 그냥 값을 넣어서 진짜로 성립되나 안되나를 본 것이라서
증명대신 2번의 성질을 이용하여 증명을 해보는 문제가 위 주소에 있습니다. 제 네이버 블로그구요. 내용은 여기꺼와 거의 같습니다.
'대학물리 > 전공물리 - [수리물리학]' 카테고리의 다른 글
| [수리물리학] Comparison Test Prove (0) | 2020.04.02 |
|---|---|
| [수리물리학] Cauchy Integral Test (코시 적분판정법) (0) | 2020.04.02 |
| [수리물리학] 라비(라베)의 판정법 (Raabe's Test) (0) | 2020.03.28 |
| [수리물리학] 쿠머 판정법 (Kummer's Test) (0) | 2020.03.28 |



