광학에서 나름 어려운 파트에 속합니다. 간섭과 회절 파트인데요. 일단 보강 간섭과 상쇄 간섭을 본 뒤 천천히 회절을 봅시다.
먼저 보강간섭의 정의는, 위상차가 같은 사인파, 코사인파 같은 그래프가 서로 다가와 만나게 될 시 더 큰 진폭을 얻는다는 말입니다.

이를 이해하기 위해서 먼저 고정단 반사 & 자유단 반사 그리고 위상차에 대해서 알아보도록 합시다.
1) 고정단 반사 : 얇은 실로 된 줄과 두꺼운 철사 줄이 같이 직렬로 묶여 있다고 생각합시다. 이 때, 얇은 실로 된 줄에서 파동이 일어났습니다. 이는 두꺼운 철사 줄 쪽으로 진행하는데 두꺼운 철사 줄에 의해 '튕겨져' 되돌아 옵니다.
이 때의 위상차는 변함이 없습니다. 이게 고정단 반사의 특징입니다.
2) 자유단 반사 : 반대로 두꺼운 철사 줄에서 얇은 실로 된 줄로 파동이 진행된다고 생각합시다. 그러면 직관적으로 생각했을 때, 두꺼운 철사 줄에서의 파동은 얇은 실로 된 줄로 진행은 합니다. 근데 여기서 일부는 다시 되돌아 오는데 이 때의 위상차는 '180도'만큼 차이가 납니다. 이게 자유단 반사의 특징입니다.
그래프 보시면 알겠지만 보강간섭은 파동1과 파동2가 서로 '같은 위상'상태일 때 결합하여 더 큰 진폭을 얻었습니다.
상쇄간섭은 '반대 위상'일 때 서로 결합한 거라 거의 소멸상태로 남습니다. 이를 '이중 슬릿'을 통해 빛의 간섭을 스크린에 나타내보면 다음과 같습니다.

보시면 어두운 부분에서는 오목하고 밝은 부분(파랑)에서는 볼록합니다. 위 그림에서 나왔듯이 실험의 이름은
영의 이중슬릿 실험입니다. 빛의 간섭에 대한 것인데요. 공식은 다음과 같습니다.

y_m은 스크린에서 가장 밝은 부분의 중심으로부터 떨어진 거리를 말합니다. 그러니까, 위 그림을 보면 원점O에서 가장 밝다고 표시되있죠? 이 밝은 부분을 중심으로 위아래로 밝,어,밝,어,밝,어... 이런 패턴이 반복됩니다. 만약 제가 중심으로부터 위에서 세번째 밝은 부분에 대한 값을 알고싶어요. 이 때 파장이랑 파장의 정수, 이중슬릿의 거리, 이중슬릿과 스크린 사이의 거리가 주어졌다면 중심과 세번째 사이의 거리를 구할 수 있겠죠?
영의 간섭 공식은 sin세타의 값과 R값을 비교했을 때 R이 매우 클 때 사용하는 공식입니다. 따라서, 세타의 크기를 무시할 수준이 안된다면 다음과 같은 공식이 나옵니다.
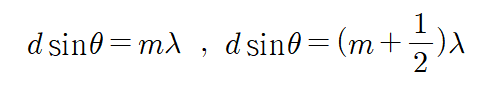
보강 간섭은 정수배고 상쇄간섭은 +1/2가 되있습니다. 왜 그러냐면 보강 간섭은 위상차가 0이지만 상쇄간섭은 위상차가 파이만큼 존재하기 때문입니다. 이에 대한 공식유도는 제가 다음에 추가로 자세히 알려드릴게요.
'대학물리 > 일반물리 - [광학]' 카테고리의 다른 글
| [광학] 1차원 파동함수 (1D Wave Function) / 편미분 방정식 (PDF) (0) | 2020.03.30 |
|---|---|
| [광학] 거울 & 렌즈 작도법 쉽고 완벽히 설명 <반드시 구독하세요> (0) | 2019.12.15 |
| [광학] 렌즈방정식 (거울상과의 비교) (0) | 2019.11.23 |
| [광학] 구면거울에 의한 상 (볼록거울과 오목거울) & 거울방정식 (0) | 2019.11.04 |
| [광학] 평면거울에 의한 상 (0) | 2019.10.29 |


