▶ 빛은 어떤 '물질'인가?
- 빛을 물질이라고 표현하기에는 다소 어색함이 들겁니다. 그러나, 빛을 딱 무엇이다! 라고 정의하기에는 사실상 이것도 맞는거같고.. 저것도 맞는거 같고.. 해요!
빛은 파동성과 입자성 둘다 띠고 있다는 것은 우리가 화학시간이나 맥스웰방정식 배울 때 많이 했을겁니다.
빛의 파동성을 설명하는 예로는 회절과 간섭현상이 있을거구요. 입자성의 경우는 Localization과 momentum이 있겠습니다.
▶ 1차원 파동
- 파동을 1차원으로 놓는다는 것은 간단합니다. 우리가 움직이는 물체를 피사체로 두고 사진을 찍었다고 생각합시다. 그러면 사진 속의 물체는 항상 그 자리에 고정되어있는 상태입니다. 그렇죠? 파동함수 역시 마찬가지입니다.
Ψ(x,t)로 표현하곤 하는데, 여기서 t를 0으로 두자는 겁니다. t=0의 의미는 그냥 시간이 항상 고정인 상태라는 것을 의미한다고 보면 됩니다.

근데 실제 파동이 항상 제자리에만 있는건 아닙니다. 그렇기 때문에, 우리는 실시간의 파동 진행에 대한 함수식을 나타내기 위해 '로렌츠 변환' 이라는 것을 이용합니다.

이게 그 예시입니다. 파동이 양의 x방향으로 진행한다고 할 때, 로렌츠변환식은 x'=x-vt로 표현이 가능합니다.
Ψ(x,t)=f(x')=f(x-vt) 이런 꼴이 되겠죠? 이제, 이 파동함수를 가지고 시간에 대한 식과 위치에 대한 식으로 각각 편미분을 함으로써 우리가 아는 파동방정식 꼴을 증명해보도록 합시다.

여기까지가 1차 편미분방정식이구요. 다음은 2차를 보도록 합시다.

이러한 꼴로 나타낼 수 있습니다. 그러면 두 2계 편미분방정식 사이의 관계를 이렇게 표현할 수 있겠죠?
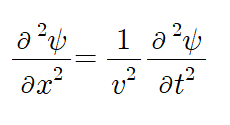
자, 이게 1차원에서의 파동방정식입니다. 이 방정식은 '고정'된 상태입니다.
'대학물리 > 일반물리 - [광학]' 카테고리의 다른 글
| [광학] Hecht 9단원 <간섭> : 간섭항과 복사조도 (0) | 2020.06.02 |
|---|---|
| [광학] 하늘은 왜 파랄까? (Feat. 레일리 산란 Rayleigh Scattering) (0) | 2020.05.11 |
| [광학] 거울 & 렌즈 작도법 쉽고 완벽히 설명 <반드시 구독하세요> (0) | 2019.12.15 |
| [광학] 이중슬릿에서의 보강 간섭과 상쇄 간섭 (0) | 2019.11.23 |
| [광학] 렌즈방정식 (거울상과의 비교) (0) | 2019.11.23 |



