가우스 법칙을 설명하기에 앞서 먼저 전기선속에 대한 이야기를 해야합니다. 전기선속은 전기력선 다발이라고 생각하시면 됩니다. 자세히 말하면 어떠한 단면적을 통과하는 유한한 전기력선 다발인데 아래 그림을 봅시다.
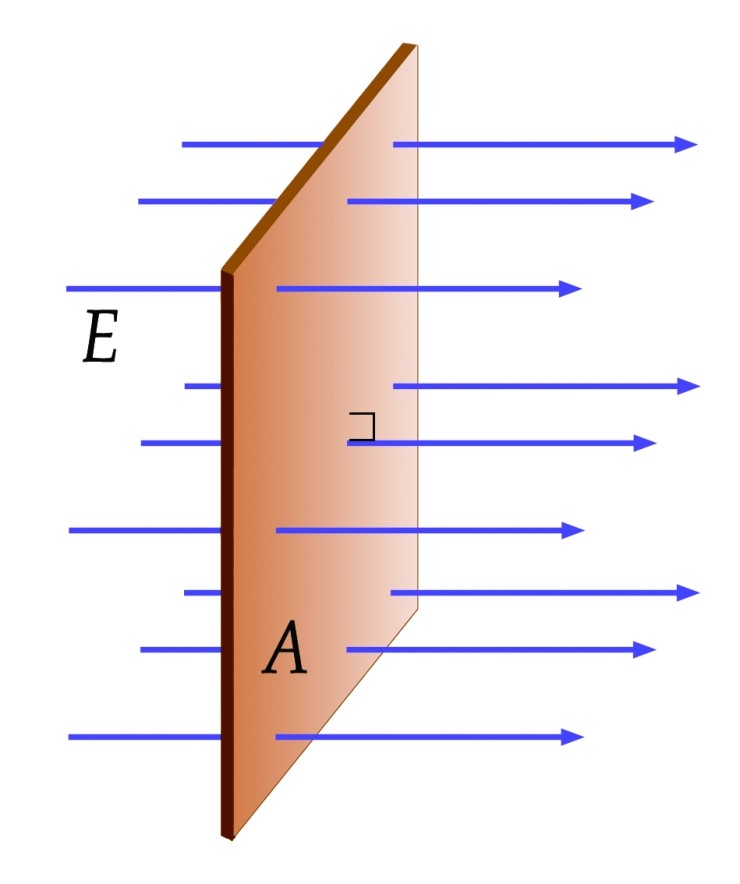
다음과 같은 그림이 있을 때, 우리는 Φ (파이라고 읽습니다.)은 E와 A의 벡터 내적과 같다. 라고 정의합니다.
파이는 전기선속을 의미합니다. 전기장과 단면적의 벡터 내적이므로, 전기장*단면적*cos세타가 됨을 알 수 있습니다.
비록 위 그림에서는 전기장과 단면적의 방향이 서로 같아 세타가 0이지만 꼭 같은 상황만 있는 것은 아니니 염두해 두기로 합니다. 세타가 0도일 때는 전기선속의 값은 EA로 max값 입니다. 그리고 90도일 때는 전기선속의 값은 0입니다. 한편, 세타가 180도 일때는 전기선속의 값은 -EA로 방향이 반대입니다.
다만 모든 면적이 저렇게 간단하게 나와있진 않는데 좀 더 다양한 물체에서의 전기선속을 구하고자 탄생한 법칙이 바로 가우스 법칙입니다. 가우스 법칙은 다음 공식을 따릅니다.
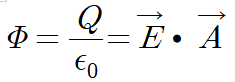
가우스 법칙은 모든 상황에서 적용되는 것은 아닙니다. 2가지 조건이 성립되야 하는데 다음과 같습니다.
1) 균일한 전기장이여야 한다.
2) 대칭적인 폐곡면으로 설정해야 한다.
아직 개념이 잘 안잡히실수도 있기에 가우스 폐곡면이 무엇인지 다시 한번 짚고 가겠습니다. 전기장은 수많은 물체들을 통과하게 됩니다. 근데 물체란 것이 99%는 비대칭적이고 균일하지 않은게 많기 때문에, 임의로 우리가 균일하고 대칭적인 면을 설정해줌으로써 전기선속을 구하려는 것입니다. 이 임의의 면. 가상의 면을 가우스 폐곡면이라 합니다.

<위 그림의 출처 - 티스토리 블로그 'appleii'>
이에 따라 선전하와 면전하도 여러분들이 적용할 수 있을겁니다. 다만, 선전하와 면전하의 경우는 점전하와 달리 연속적인 전하 분포를 띠고 있기 때문에 선전하밀도와 면전하밀도 개념을 도입해야 합니다.

'대학물리 > 일반물리 - [전자기학]' 카테고리의 다른 글
| [전자기학] 옴의 법칙과 직렬&병렬 회로 (0) | 2019.09.14 |
|---|---|
| [전자기학] 전류와 기전력(Electromotive force) (0) | 2019.09.14 |
| [전자기학] 축전기와 전기용량 (캐패시턴스) (0) | 2019.09.14 |
| [전자기학] 전위와 전위차 (0) | 2019.09.14 |
| [전자기학] 전기력(Electronic Force)과 전기장 (Electronic Field) (0) | 2019.09.13 |


