데이터분석은 제조업에서 수율개선 및 공정 개선점을 발견하는데 좋은 이정표가 되어줍니다. 디스플레이 하나를 만드는데 수많은 공정데이터가 쌓이게 되는데요. 이러한 데이터표본을 컴퓨터에게 제시해주고 정답을 찾기 위한 가이드라인. 메뉴얼까지 제공하여 학습을 시키는 것이 머신러닝입니다.
반대로 딥러닝은 데이터표본만 컴퓨터에게 던져주면, 컴퓨터가 알아서 가이드라인을 짜고 분류를 하여 학습을 시작합니다.
머신러닝의 대표적이면서도 핵심 예시는 선형회귀분석입니다.
1차 선형함수로 되어있고, 결과값을 y라 한다면 x는 데이터 값들을 의미하구요. 기울기 a는 가중치를, 절편 b는 보정치를 의미합니다.

빨간색 선은 주어진 데이터표본에 가장 최적화된 기울기 값을 찾기 위해 가설을 세운 것들입니다. 물론 우리 눈에는 어떤 기울기가 제일 적합한지 보이지만, 컴퓨터는 아직 모르기에 이런 식으로 가설들을 세웁니다.
(최적화되었다는게 오차 0를 의미하는 것은 아닙니다.)
'코딩애플' 이라는 유튜브에서 참고했던 내용인데 예시를 너무 잘 들어주셔서 인용하면서 복습해보고자 합니다.
수능성적을 예측하기 위해서 3월부터 10월 모의고사까지의 성적을 참고하고자 합니다.
| 수학 모의고사 | 가중치 | 결과값 |
| 3월 - 68점 | 0.05 | ?? |
| 4월 - 66점 | 0.05 | |
| 6월 - 84점 | 0.3 | |
| 7월 - 84점 | 0.1 | |
| 9월 - 92점 | 0.4 | |
| 10월 - 88점 | 0.1 |
이렇게 주어졌어요. 그러면 여기서 데이터 값은 x라하고 w (기울기)는 가중치가 됩니다.

이런 상태에요. 그러면 저거 일단 계산을 먼저 해봅시다.
3월 = 68*0.05 = 3.4
4월 = 66*0.05 = 3.3
6월 = 84*0.3 = 25.2
7월 = 84*0.1 = 8.4
9월 = 92*0.4 = 36.8
10월 = 88*0.1 = 8.8
y = w1*x1 + w2*x2 + w3*x3 + w4*x4 + w5*x5 + w6*x6 = 85.9점 즉, 수능 수학 성적을 86점이라고 예측을 했습니다.
가중치 값은 저희가 임의로 넣은거에요. 보통 평가원모의고사 6,9월께 중요하잖아요? 28살 아죠씨라 수능친지는 까마득하지만 ㅎㅎ;;;
근데 실제 수능 수학점수가 92점이 나왔다? 그럼 오차값이 6점이나 나죠? 그럼 이제 여기서 컴퓨터가 가중치를 바꿔도 보고, 보정값 b를 넣어주면서 이 오차값을 최소한 줄이고자 노력합니다.
그 가중치를 바꾸기 위한 공식을 cost reduction이라 합니다. cost (w,b)로 표현을 하는데요. 간단합니다.
실제값 y1과 예측값 y2 사이의 차이들의 total sum을 구합니다. 그 sum에다 '제곱'을 한 뒤, 그걸 데이터 표본개수로 나눕니다.

수식으로 치면 이런거죠. 제곱을 해주는 이유. 이걸 평균제곱오차라 하는데, 예측값 (위에 ^ 달린 애)이랑 실제값의 차이가 음수거나 양수일 때가 있습니다. 이걸 제곱을 안해주고 더해버리면 오히려 total sum값이 0에 가까워지는 이슈가 발생해요. 오차는 실제로 많이 났는데 정확성이 높다! 라고 판정해버리는거죠. 그래서 제곱을 해주는 겁니다.
머신러닝을 더 깊게 들어가면 글이 너무 길어지니까, 일단 딱 여기까지만 다루고요. 딥러닝은 어떤지 이걸 이어서 생각해보겠습니다.
머신러닝은 위처럼 가중치와 보정값으로 구성되어있는데, 딥러닝도 똑같습니다. 가중치와 보정값이 있는데 여기에 추가로 '상황별 케이스'를 고려합니다. 즉, Input Layer와 Output Layer로 이뤄진 퍼셉트론에서 이 중간에 'Hidden Layer'라는 노드가 추가됩니다. 이러한 딥러닝 퍼셉트론들이 모이고모인게 '뉴럴 네트워크'입니다.

대충 그림 그려봤습니다. 중간에 추가된 노드들을 Hidden Layer라고 합니다. 즉, 여기선 3가지 케이스를 염두해두고 Input Layer에서 임의의 가중치를 두고 계산해낸 값을 H1에 저장했다. 또 다른 가중치를 두고 계산해낸 값을 H2, H3에 각각 저장했다. 라고 볼 수 있습니다.
그렇게해서 다양한 '케이스'들을 고려해서 도출해낸 결과값이 이겁니다~ 하는게 딥러닝. 인데.
그냥 Hidden Layer 하나 추가했다고 머신러닝이 갑자기 딥러닝이 되고 그런건 아닙니다.
이 Hidden Layer에서 추가되는게 바로 활성 함수입니다. (Activation Function)
활성 함수는 여러개가 있겠지만, 많이 쓰이고 이것만큼은 알아가야한다는게 몇개 있어서 꼽아 봤습니다.
1) 시그모이드
Binary 분류의 대표적인 함수로 보통 출력층에서 자주 사용됩니다. 0과 1 사이의 범위값을 가지므로 보통 '확률'을 보여줄 때 씁니다.

시그모이드 함수의 원형입니다. x축 데이터들을 입력하면 결과값은 0과 1사이의 실수로 출력됩니다. 시그모이드는 사실
그리 좋은 함수는 아닙니다. Vanishing Gradient Problem이라 해서 고질적인 Output층의 신뢰도 하락을 일으키는게 있는데요. 굉장히 많은 Input층을 0과 1이라는 범위 내로 '우겨넣는' Activation Function때문에 Input에서 큰 변화가 일어나도 Output에서는 그 변화가 미미하기 때문입니다.
또한, 시그모이드는 데이터가 많으면 많을수록 그리 효율성이 좋지 않아 현업에선 잘 쓰지않습니다. 마치, 버블소트 알고리즘처럼 '교육용 입문개념'에 그쳐있습니다.
시그모이드와 같이 교육에서만 다루는 활성함수가 하나 또 있습니다.
2) tanh (하이퍼볼릭 탄젠트)
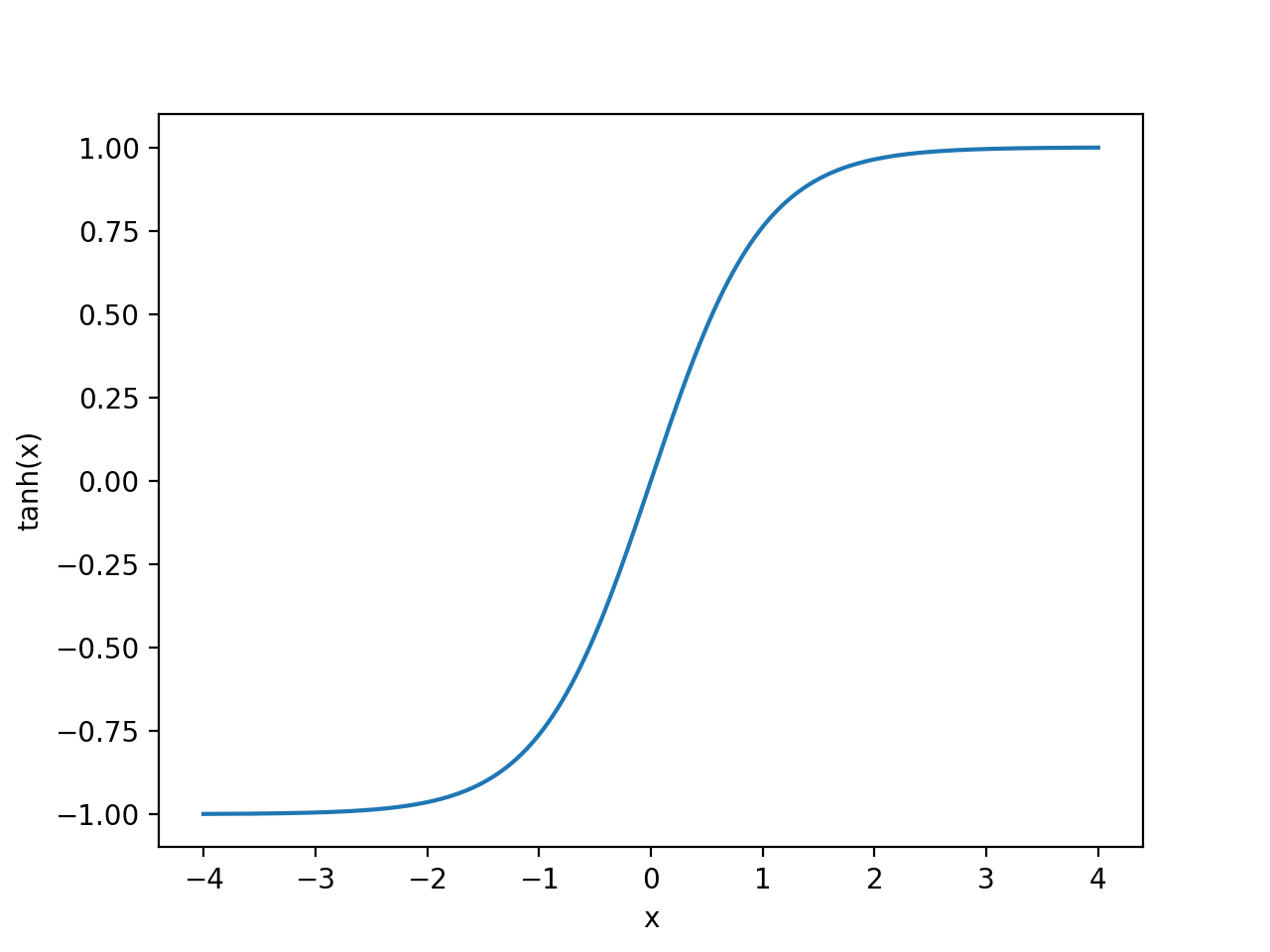
얘도 Input 데이터는 방대한데, Output은 [-1,1]로 굉장히 짓이겨놓은 식입니다.
요약
- 시그모이드와 tanh는 Output의 범위를 짓이겨놓았기 때문에 Input에서 큰 변화가 있더라도 Output에선 경미하게 발생한다.
그럼 어떤 함수를 쓰는게 좋냐? 대표적인게 ReLu입니다.
3) ReLu
- Relu의 원형은

음수 데이터값은 그냥 모두 0으로 반환하고, 양수 값에는 제한이 없는 상태로 둡니다.
따라서, 데이터를 짓이겨넣음으로써 발생하는 기울시 소실 (Vanishing Gradient Problem)을 막을 수 있어요.
또한, 기울기가 일정하기 때문에 가중치 업데이트도 다른 함수보다 훨씬 빠릅니다. 뭐 비선형성을 띠는 함수들은 가중치 업데이트에서 시간이 좀 걸리는데 얘는 간단하니까요!
다만, ReLu는 Hidden Layer층에서만 사용하는걸 권장하는 편입니다.
가중치 업데이트 과정에서 total sum이 0이 되면 그 뒤론 계속 0만 반환합니다. 즉, 죽어가는 뉴런이 되어버리는거에요.
따라서 Output층엔 쓰면 안됩니다. 차라리, ReLu로 Hidden Layer층 활성화시키고, Output층으로 계산때릴 때, 결과값이 뭐 0과 1 사이의 확률로 나타내야한다! 하면 시그모이드를 채택하는게 적합할 것입니다.
* 경사하강법
마지막으로 짚고 갈 것은 경사하강법입니다. 비선형 데이터함수가 주어졌다고 가정해봅시다.

이런 cost가 주어졌다 합시다. 이 함수 그래프에서 C는 cost를 의미하고 y는 가중치를 의미합니다. 아무 사진이나 갖고온거라 변수는 다를 수 있지만 아무튼 x축이 가중치 y축이 cost다! 라고 보시면 되겠습니다.
맨 처음에는 제일 왼쪽에 있는 빨간색 지점에 가중치를 뒀다 생각해봅시다. 근데 cost 비용이 상당히 큽니다. 딱 봤을 때,
Best! 부분이 가장 낮은 cost값을 갖고 있어요. 그럼 어떻게해야하나? cost를 낮추는 방향으로 움직여야 합니다.
그 방향을 어떻게 정해주느냐? 일단 기울기가 양과 음이 바뀌는 그 순간에 주목해봅시다. 양과 음이 바뀌는 그 순간은 기울기 값이 0입니다.
따라서, 현재 임의로 지정한 가중치가 '음의 기울기'라면요? 양의 기울기가 되도록 값을 더하게 될 것입니다.

빨간부분에 해당하는 파란색 함수의 w1값과 초록색 선형근사 함수의 기울기값. 이 2개를 합하면 됩니다.
즉, 음의 기울기인 경우 선형근사식의 기울기 + w1로 하면 0값에 가까워지니까요.
그럼 눈치 빠르신분은들은 양의 기울기인 경우에는 선형근사식의 기울기 - w1로 하면 0값에 가까워지니까
이를 그림으로 생각해보면 기울기가 0인 지점을 향해 달려가는 '경사하강하는 모습'이 되지 않겠습니까?
근데, 이걸로 끝이 아닙니다. 위에 그린 함수처럼 local적인 부분에서 minimum인 지점이 있어요. 인간이 보기엔 딱 봐도 최소비용 지점이 보이는데 컴퓨터는 경사하강을 진행하다보면 기울기가 0이네? ㅇㅋ 여긴가보다~ 하고 멈추거든요.
그래서 등장한게 'Learning Rate'개념입니다.
말 그대로 경사하강에 대한 비율을 정해주는 것입니다. Learning Rate가 많이 작으면 정밀하게 기울기 0값을 향해 찾아가겠지만 Local Minimum을 피하긴 어렵습니다. 쉽게 말해서 함정을 '점프'해가는 슈퍼마리오같은애라 보면 됩니다.
그래서 적절한 Learning Rate값을 찾아주는 것도 또 하나의 중요한 포인트입니다. 과하지도, 부족하지도 않은게 좋거든요.
근데 딥러닝에선 keras가 이거 다 알아서 해줍니다 ㅋ
아무튼 여기까지 개념복습을 마치겠습니다.
'프로그래밍 > Python' 카테고리의 다른 글
| [Python] # 0. 파이썬 기초 문법 Review (1) (0) | 2023.01.03 |
|---|---|
| [Python] # 3. 리스트, 튜플, 딕셔너리 (0) | 2022.06.12 |
| [Python] # 2. 숫자형,문자열 슬라이싱에 대한 쉬운 정리 (0) | 2022.05.30 |
| [Python] # 1. 딥러닝을 활용한 데이터분석 모델 구현 복습 (0) | 2022.05.01 |

